荣耀的博客

更多变换

发表于 分类于

正交矩阵

上节课已经知道, 旋转的变换矩阵为

Rθ=[cos⁡θ−sin⁡θsin⁡θcos⁡θ]R_\theta = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}

当θ为负, 即反向(顺时针)旋转的变换矩阵为

R−θ=[cos⁡θsin⁡θ−sin⁡θcos⁡θ]R_-\theta = \begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix}

可以发现

R−θ=Rθ−1=RθTR_{-\theta} = R_\theta^{-1} = R_\theta^T

即旋转矩阵的逆矩阵等于其转置矩阵, 数学上称这样的矩阵为正交矩阵

3D 旋转

绕轴旋转

  1. 绕x 轴

    Rx(α)=[10000cosα−sinα00sinαcosα00001]R_x (\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha & 0 \\ 0 & sin\alpha & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}

  2. 绕y轴

    Ry(α)=[cosα0sinα00100−sinα0cosα00001]R_y (\alpha) = \begin{bmatrix} cos\alpha & 0 & sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -sin\alpha & 0 & cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}

    注意 z×x=y,x×z=−yz \times x = y, x \times z = -y , 此处的 sinαsin \alpha 和 −sinα-sin \alpha 需要调换

  3. 绕z轴

    Rz(α)=[cosα−sinα00sinαcosα0000100001]R_z (\alpha) = \begin{bmatrix} cos\alpha & -sin\alpha & 0 & 0 \\ sin\alpha & cos\alpha & 0& 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}

绕任意轴旋转

任意旋转可以分解为绕轴旋转的叠加

Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ)R_{xyz} (\alpha, \beta, \gamma) = R_x(\alpha) R_y(\beta) R_z(\gamma)

罗德里格斯旋转公式 Rodrigues’ Rotation Formula

给定旋转角度 α\alpha 和旋转轴 nn

Rn,α=cos⁡(α)I+(1−cos⁡(α))nnT+sin⁡(α)[0−nznynz0−nx−nynx0]R_{n, \alpha} = \cos (\alpha) I + (1 - \cos (\alpha))nn^T + \sin (\alpha) \begin{bmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{bmatrix}

视图/相机变换 view / camera transformation

如何定义一个相机?

  1. 位置 e⃗\vec e
  2. 看的朝向 g^\hat g
  3. 向上的方向 t^\hat t

思考

物体和相机做相同的变换后, 得到的结果不变

约定:
相机永远位于原点, 看向-z方向, 向上为y轴

如何从任意坐标转换到约定的相机坐标系?

  1. 将e⃗\vec e平移到相机坐标系的原点
  2. 将g^\hat g旋转到相机坐标系的-z方向
  3. 将t^\hat t旋转到相机坐标系的y方向
  4. 将g^×t^\hat g \times \hat t旋转到x方向

使用矩阵表示, 即:

Mview=RviewTviewM_{view} = R_{view}T_{view}

其中, TviewT_{view} 表示平移到原点

Tview=[100−xe010−ye001−ze0001]T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix}

然后旋转; 由于从g到-Z, t到Y, g^×t^\hat g \times \hat t 到 X 较为复杂, 尝试写出它的逆变换:

Rview−1=[xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001]R_{view}^{-1} = \begin{bmatrix} x_{\hat g \times \hat t} & x_t & x_{-g} & 0 \\ y_{\hat g \times \hat t} & y_t & y_{-g} & 0 \\ z_{\hat g \times \hat t} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

又旋转矩阵为正交矩阵, 则:

Rview=[xg^×t^yg^×t^zg^×t^0xtytzt0x−gy−gz−g00001]R_{view} = \begin{bmatrix} x_{\hat g \times \hat t} & y_{\hat g \times \hat t} & z_{\hat g \times \hat t} & 0 \\ x_t & y_t & z_t & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

投影变换 Projection transformation

正交投影 Orthographic Projection

定义: 一个立方体, 其左右/上下/前后边界为: [l, r]/[b, t]/ [f, n], 将其映射到 [−1,1]3[-1, 1]^3(被称为canonical cube: 标准立方体) 的立方体上

由于向-z方向看, f和n是相反的

做法: 先平移立方体中心到原点, 再缩放
矩阵表示:

Mortho=[2r−l00002t−b00002n−f00001][100−r+l2010−t+b2001−n+f20001]M_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}

透视投影 Perspective Projection

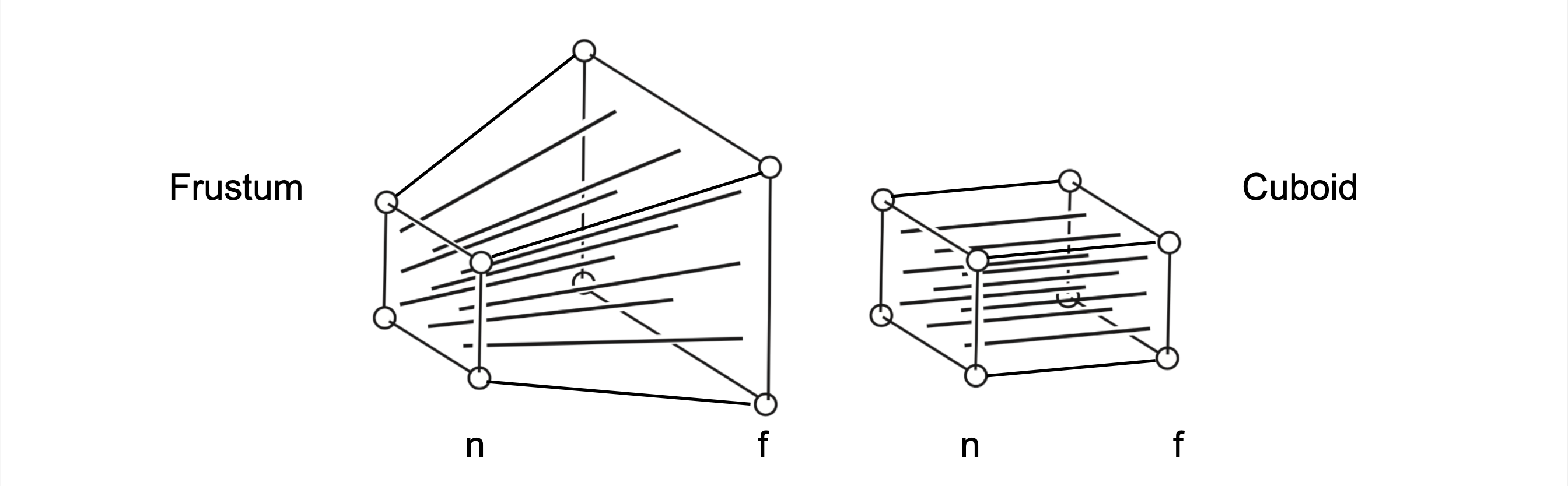
做法: 将一个任意立方体, “挤压” 成一个边垂直的立方体, 然后做正交投影, “挤压”时, 近平面上的点不变

从侧面看

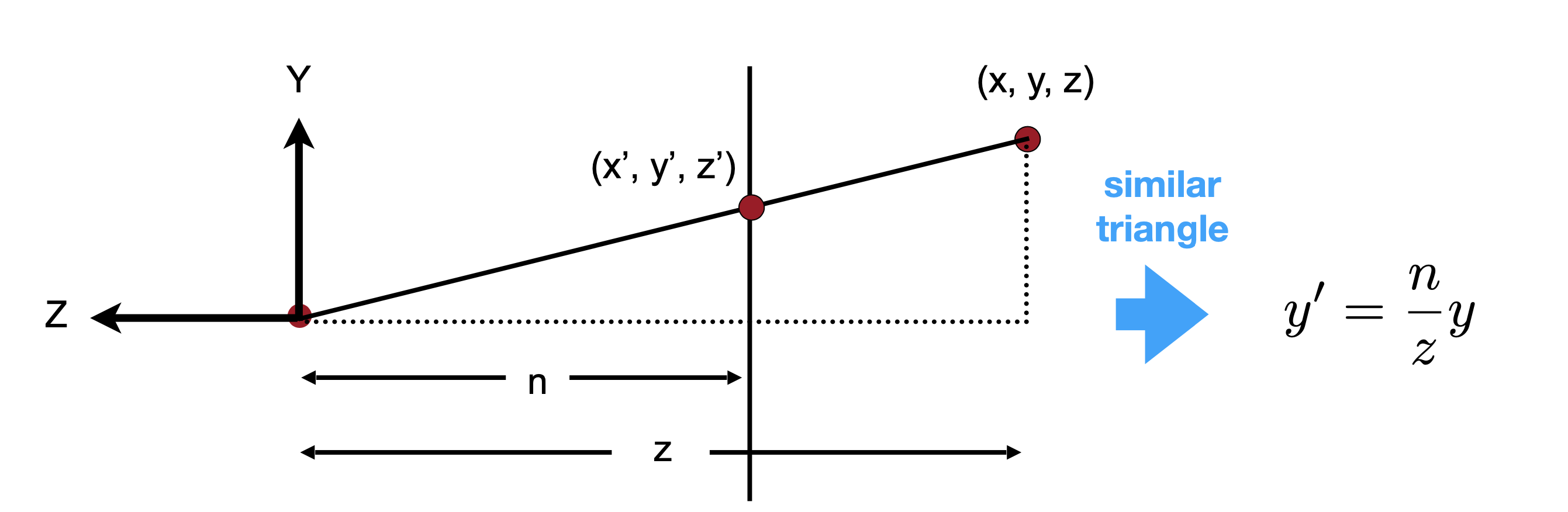
可以得到

(xyz1)→(nxznyz?1)→同时乘z(nxny?z)\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \rightarrow \begin{pmatrix} \frac{nx}{z} \\ \frac{ny}{z} \\ ? \\ 1 \end{pmatrix} \xrightarrow{同时乘 z} \begin{pmatrix} nx \\ ny \\ ? \\ z \end{pmatrix}

尝试填充变换矩阵

Mpersp→ortho=(n0000n00????0010)M_{persp \rightarrow ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{pmatrix}

据观察

  1. 近平面上的点不变 (xyn1)⇒(xyn1)==(nxnyn2n)\begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} == \begin{pmatrix} nx \\ ny \\ n^2 \\ n \end{pmatrix}
    所以, 第三行 (00AB)(xyn1)=n2\begin{pmatrix} 0 & 0 & A & B \end{pmatrix} \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} = n^2
  2. 远平面上的 z 不变 (00f1)⇒(00f1)==(00f2f)\begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} == \begin{pmatrix} 0 \\ 0 \\ f^2 \\ f \end{pmatrix}

    综上
    An+B=n2Af+B=f2}→A=n+fB=−nf\left. \begin{aligned} An + B = n^2 \\ Af + B = f^2 \end{aligned} \right \} \to \begin{aligned} A & = n + f \\ B & = -nf \end{aligned}

最终得到

Mpersp→ortho=(n0000n0000n+f−nf0010)M_{persp \rightarrow ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix}

系列说明


本系列文章 是 @Lingqi Yan(闫令琪) 教授《现代计算机图形学入门》 视频课程的文字笔记, 方便各位图形学爱好者朋友学习巩固使用

原课程链接: GAMES101: 现代计算机图形学入门
同时, 该教程已上传哔哩哔哩, 链接: GAMES101-现代计算机图形学入门-闫令琪

附

课件源文件： GAMES101_Lecture_04.pdf
哔哩哔哩视频传送门： GAMES101-现代计算机图形学入门-闫令琪