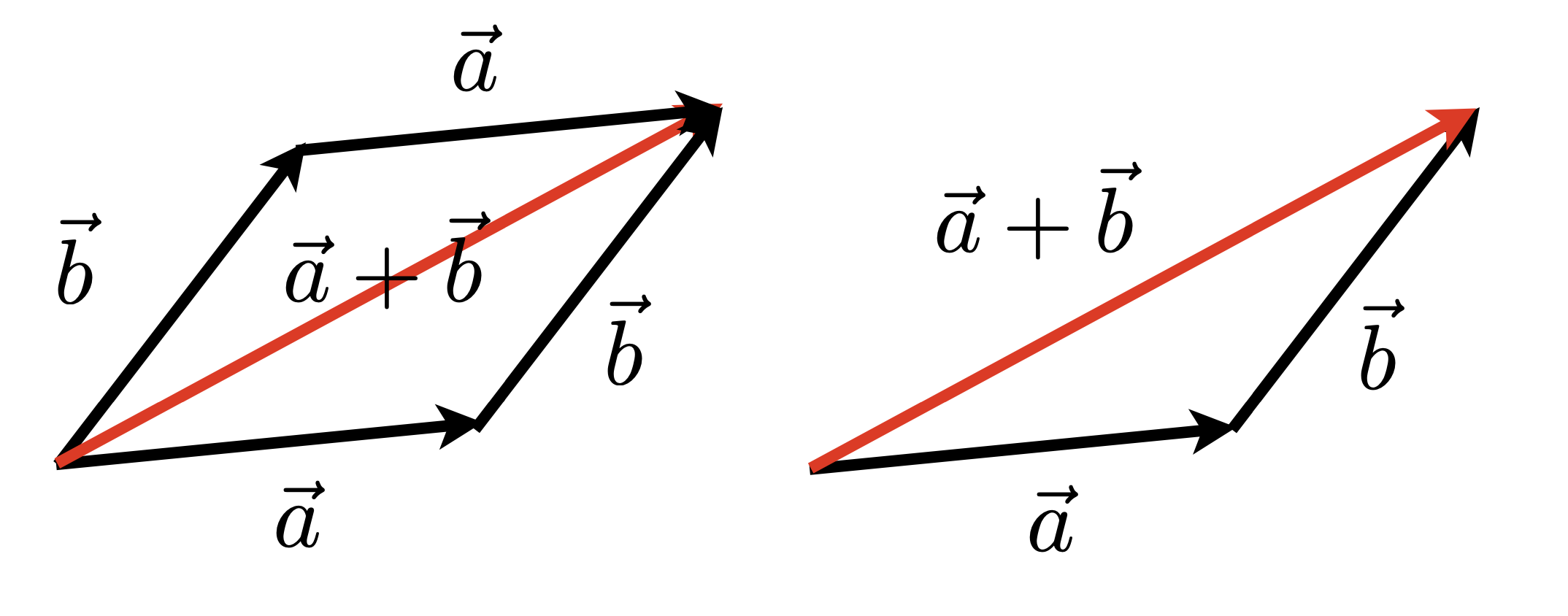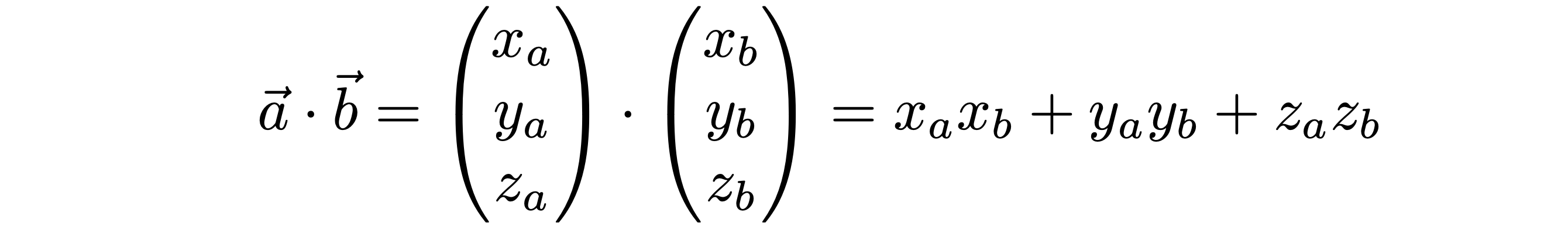荣耀的博客

数学基础(线性代数)

发表于 分类于

向量 Vectors

  • 有大小, 有方向
  • 常写作 a⃗\vec a 或者 a\boldsymbol a (加粗字母)
  • 或者使用 AB→=B−A\overrightarrow {A B} = B - A 表示从起始点到目标点的向量
  • 不关心绝对的开始和结束位置
  • 向量长度用 ∣∣a⃗∣∣|| \vec a || 表示
  • 单位向量
    • 向量长度为 1
    • 用 a^\hat a 表示, 常用 a^=a⃗∣∣a⃗∣∣\hat a = \frac{\vec a} {|| \vec a ||} 获得单位向量
    • 可以用来只表示方向

向量求和

  • 几何方法

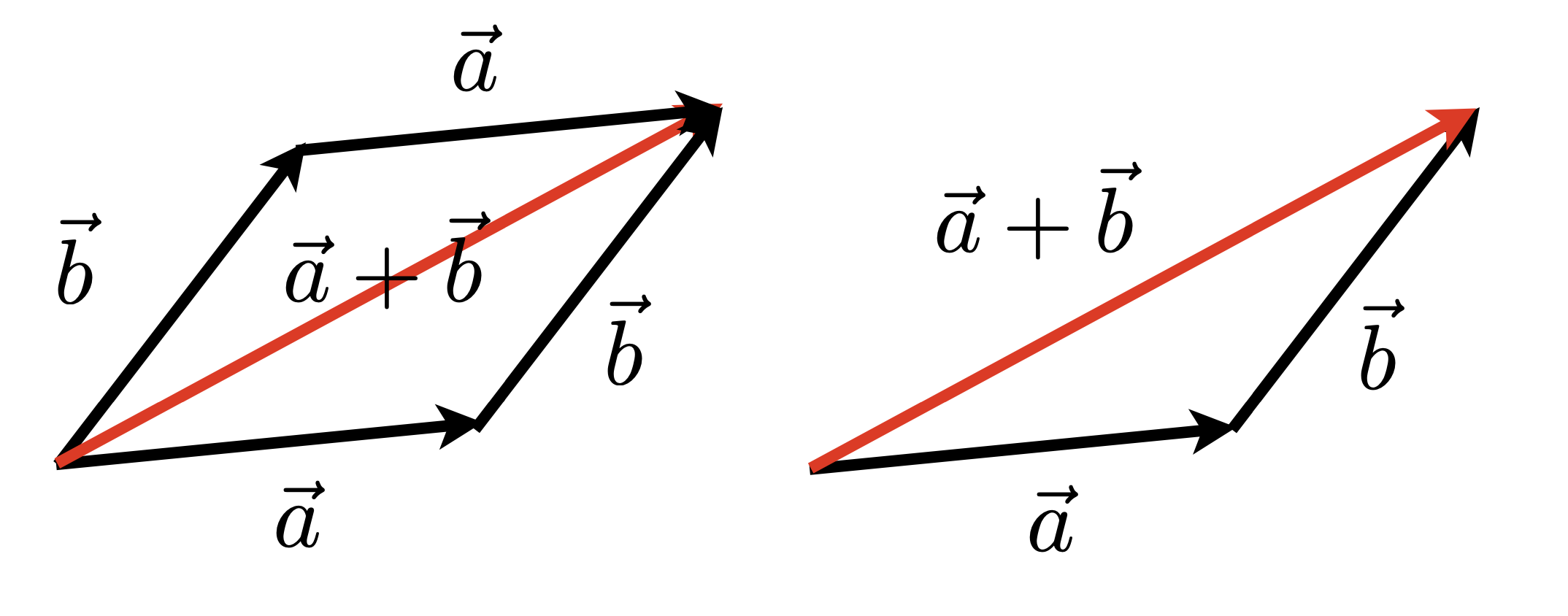
    平行四边形法则: 两个向量合成时，以表示这两个向量的线段为邻边作平行四边形，这个平行四边形的对角线就表示合向量的大小和方向
    三角形法则: 两个向量合成时, 将向量首尾相接, 从第一个向量的头指向第二个向量的尾的向量即是和向量, 即 AB→+BC→=AC→\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}

  • 代数方法
    对应坐标相加

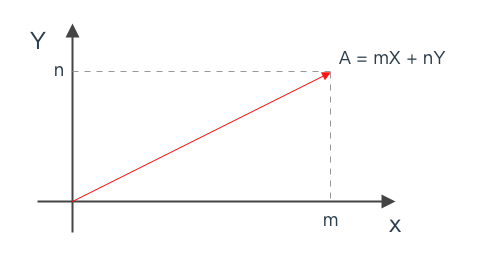
    向量也常会使用分解到(笛卡尔坐标系)x 轴和 y 轴的两个向量的和表示, 即 A=mX+nYA = mX + nY

    • 图形学中, 一般使用列向量来表示向量, 即 A=[xy]A = \begin{bmatrix} x \\ y \end{bmatrix}
    • 这样表示可以更方便的计算向量的长度, 即 ∣∣A∣∣=n2+m2||A|| = \sqrt {n^2 + m^2}

向量乘法

点乘

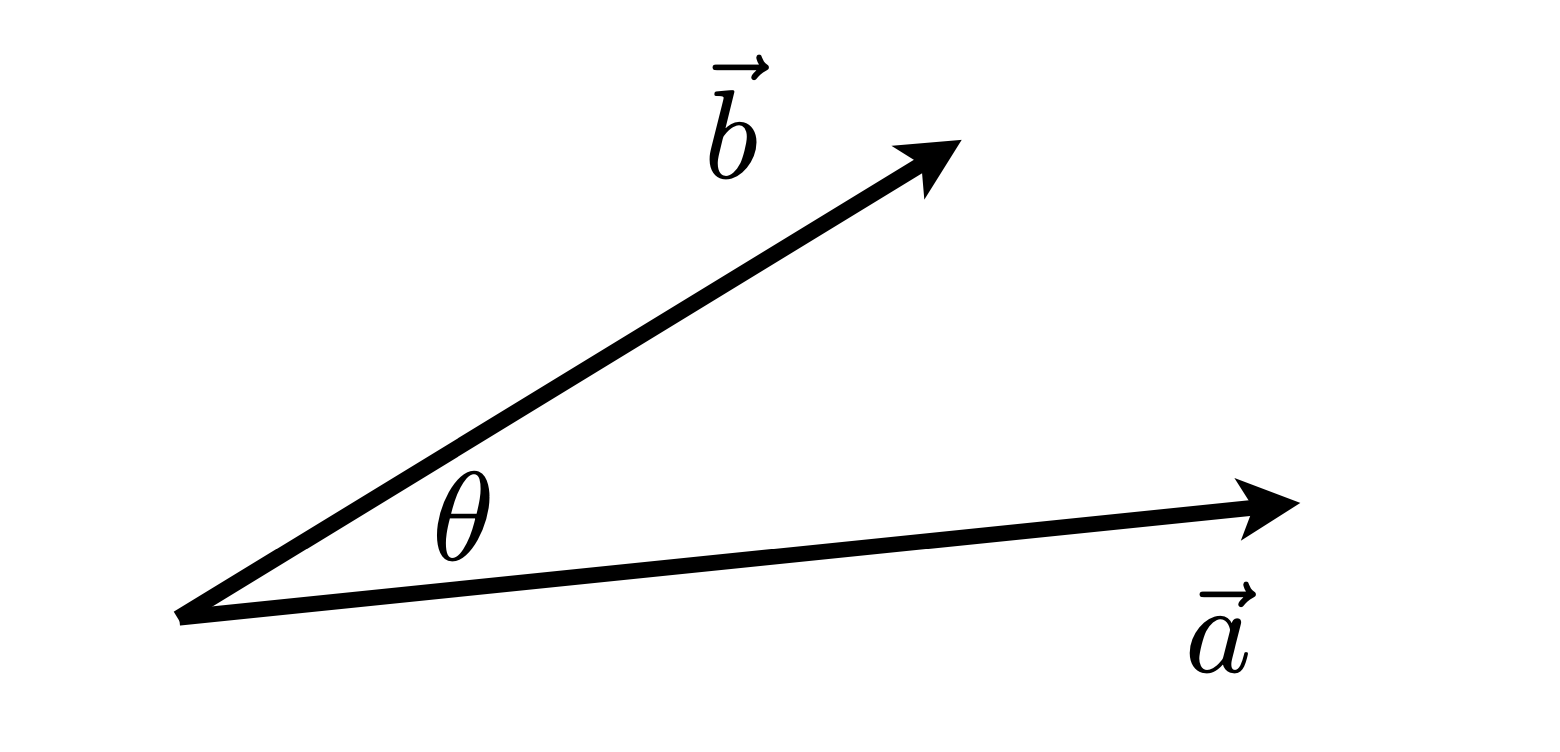
  • a⃗⋅b⃗=∣∣a⃗∣∣⋅∣∣b⃗∣∣⋅cosθ\vec a \cdot \vec b = ||\vec a||\cdot||\vec b|| \cdot cos \theta
  • cosθ=a⃗⋅b⃗∣∣a⃗∣∣⋅∣∣b⃗∣∣cos \theta = \frac{\vec a \cdot \vec b} {|| \vec a || \cdot || \vec b ||}
  • cosθ=a^⋅b^cos \theta = \hat a \cdot \hat b
  • 坐标系上的计算
    • 2D
    • 3D

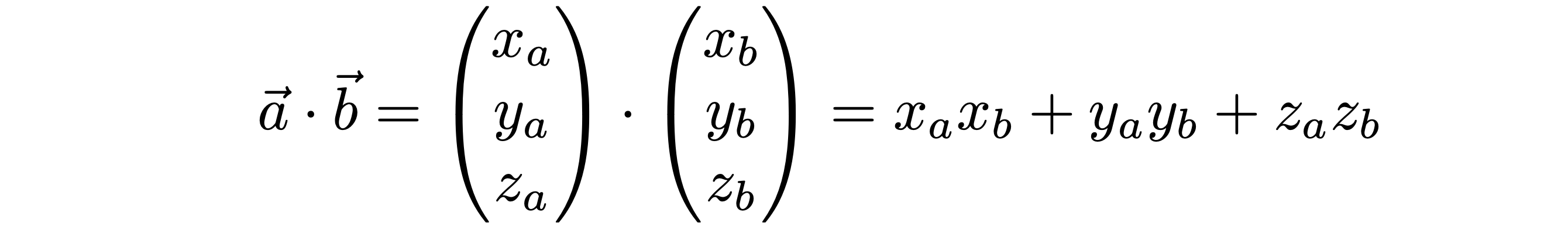
性质

  • 交换律 a⃗⋅b⃗=b⃗⋅a⃗\vec a \cdot \vec b = \vec b \cdot \vec a
  • 结合律 a⃗⋅(b⃗+c⃗)=a⃗⋅b⃗+a⃗⋅c⃗\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec b + \vec a \cdot \vec c
  • 分配率 (ka⃗)⋅b⃗=a⃗⋅(kb⃗)=k(a⃗⋅b⃗)(k\vec a) \cdot \vec b = \vec a \cdot (k \vec b) = k(\vec a \cdot \vec b)

图形学中应用

  • 常用作找两个方向的夹角
  • 常用作计算一个向量在另一个向量上的投影
  • 分解向量
    二维分解: p⃗=(p⃗⋅u^)u^+(p⃗⋅v^)v^\vec p = (\vec p \cdot \hat u) \hat u + (\vec p \cdot \hat v) \hat v
    三维分解: p⃗=(p⃗⋅u^)u^+(p⃗⋅v^)v^+(p⃗⋅w^)w^\vec p = (\vec p \cdot \hat u) \hat u + (\vec p \cdot \hat v) \hat v + (\vec p \cdot \hat w) \hat w
  • 判断两个向量有多接近
  • 判断两个向量是否朝向同一个方向 -> 点积 > 0 或者 < 0

叉乘

  • 两向量叉乘的积是另一个向量
  • 叉积同时垂直与两个向量
  • 方向取决于右手(螺旋)定则
  • 可用作构建空间直角坐标系
    • x⃗×y⃗=+z⃗\vec x \times \vec y = + \vec z
    • y⃗×x⃗=−z⃗\vec y \times \vec x = - \vec z
    • y⃗×z⃗=+x⃗\vec y \times \vec z = + \vec x
    • z⃗×y⃗=−x⃗\vec z \times \vec y = - \vec x
    • z⃗×x⃗=+y⃗\vec z \times \vec x = + \vec y
    • x⃗×z⃗=−y⃗\vec x \times \vec z = - \vec y

性质

  • a⃗×b⃗=−b⃗×a⃗\vec a \times \vec b = -\vec b \times \vec a
  • a⃗×a⃗=0⃗\vec a \times \vec a = \vec 0
  • a⃗×(b⃗+b⃗)=a⃗×b⃗+a⃗×c⃗\vec a \times (\vec b + \vec b) = \vec a \times \vec b + \vec a \times \vec c
  • a⃗×(kb⃗)=k(a⃗×b⃗)\vec a \times (k\vec b) =k(\vec a \times \vec b)

图形学中的应用

  • 判断左右:
    左侧叉积为正, 右侧叉积为负
  • 判断内外:
    三角形三个顶点为ABC, 点为 P, 依次计算 AB→×AP→,BC→×BP→,CA→×CP→\overrightarrow {AB} \times \overrightarrow {AP}, \overrightarrow {BC} \times \overrightarrow {BP},\overrightarrow {CA} \times \overrightarrow {CP}, 若各个叉积方向相同, 则点 P 在三角形 ABC 内, 有任意叉积不同方向, 则点 P 在三角形 ABC 外

矩阵

定义: m 行 n 列的一系列数

[135204]\begin{bmatrix} 1 & 3 \\ 5 & 2 \\ 0 & 4 \\ \end{bmatrix}

矩阵和数字相乘, 结果为该数字和矩阵的每一个元素相乘组成的新矩阵

乘法

可乘 = (M x N) (N x P) = (M x P), 其他不可乘

叉乘算法: A x B = R, R[m][n]的值为: A 的第 m 行,与 B 的 第 n 列所有元素依次相乘再求和

性质

  • 不符合交换律: AB ≠ BA
  • 符合结合律和分配率
    • (AB)C = A(BC)
    • A(B + C) = AB + AC
    • (A + B)C = AC + BC

转置

[123456]T=[135246]\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} ^ T = \begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix}

性质

(AB)T=BTAT(AB)^T = B^TA^T

单位矩阵

  • I3×3=[100010001]I_{3\times3} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
  • 矩阵的逆, 定义: AA−1=A−1A=IAA^-1 = A^-1A = I
  • (AB)−1=B−1A−1(AB)^-1=B^-1A^-1

使用矩阵计算向量

点乘

a⃗⋅b⃗=[xayaza][xbybza]=(xaxb+yayb+zazb)\vec a \cdot \vec b = \begin{bmatrix} x_a && y_a && z_a \end{bmatrix} \begin{bmatrix} x_b \\ y_b \\ z_a \end{bmatrix} = (x_ax_b + y_ay_b + z_az_b)

叉乘

a⃗×b⃗=A∗b=[0−zayaza0−xa−yaxa0][xbybza]\vec a \times \vec b = A^*b = \begin{bmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{bmatrix} \begin{bmatrix} x_b \\ y_b \\ z_a \end{bmatrix}

系列说明


本系列文章 是 @Lingqi Yan(闫令琪) 教授《现代计算机图形学入门》 视频课程的文字笔记, 方便各位图形学爱好者朋友学习巩固使用

原课程链接: GAMES101: 现代计算机图形学入门
同时, 该教程已上传哔哩哔哩, 链接: GAMES101-现代计算机图形学入门-闫令琪

附

课件源文件： GAMES101_Lecture_02.pdf
哔哩哔哩视频传送门： GAMES101-现代计算机图形学入门-闫令琪